Abstract
Background: Company director networks have been studied for many countries, including South Africa, from the perspective of network theory. However, most studies of company director networks focus on the overall structure of the network, that is, by conducting a macro-level analysis.
Aim: In this study, we conducted a node-level analysis to investigate whether the four major South African banks, namely, Barclays Africa Group Ltd (now ABSA Group Limited), Nedbank Group Ltd, Standard Bank Group Ltd and FirstRand Ltd, occupy central roles in the company director network on the Johannesburg Stock Exchange (JSE).
Setting: Social networks provide a vital source of information and are therefore an important field of study in business.
Methods: We use degree-, betweenness- and closeness centrality, as well as strength, and a force-directed layout to investigate whether these four banks occupy key positions in the company director network on the JSE.
Results: We show that these four banks occupy central roles on the JSE. The direct connections of these companies are also identified, and findings are compared to some overseas studies.
Conclusion: This study concludes that the said four major banks occupy key positions on the JSE.
Introduction
Banks occupy an important role in a country’s economy, in part through their extensive connections to other companies. Through director interlocks, in particular where companies share directors, banks develop close ties with companies at the heart of an economy (Bearden et al., 1975; Farina, 2008), and although Davis, Yoo and Baker (2003) have found that banks’ centrality in the USA declined between the 1980s and 1990s, they still occupy a key role in the company director network (Mizruchi, 2007, p. 13), as also found by Williams, Deodutt and Stainbank (2016, p. 131) in the South African context.
Of course, director interlocks are not a new phenomenon; in 1904, for instance, George F. Baker, President of the First National Bank of New York, sat on the boards of 38 firms (Mizruchi, 2007, p. 11). Company director networks have been studied for over a century, and the oldest study cited by Mizruchi (2007, p. 11) is the 1913 US Congressional Report issued by the House Banking and Currency Committee, while the oldest study cited by Takes and Heemskerk (2016, p. 3) is the study by Jeidels (1905). In recent years, company director networks of numerous countries have been studied within the framework of network theory, for instance, those in the USA (Davis & Greve, 1997; Davis et al., 2003), UK (Conyon & Muldoon, 2006), Germany (Conyon & Muldoon, 2006; Kogut & Belinky, 2008; Raddant, Milaković, & Birg, 2017), France (Elouaer-Mrizak & Chastand, 2013), Ireland (Friel, Rastelli, Wyse, & Raftery, 2016), the Netherlands (Heemskerk, 2013; Heemskerk & Schnyder, 2008), Italy (Drago, Millo, Ricciutti, & Santella, 2015; Drago & Ricciuti, 2017; Farina, 2008; Piccardi, Calatroni, & Bertoni, 2010), Scandinavia (Sinani et al., 2008), various other European countries (Heemskerk, Daolio, & Tomassini, 2013), India (Shaw, Cordeiro, & Saravanan, 2016), China (Guo & Lv, 2018) and even those that are globally connected (Abdollahian, Thomas, Yang, & Chiang, 2017; Glattfelder, 2013; Takes & Heemskerk, 2016). In South Africa, the company director network on the Johannesburg Stock Exchange (JSE) was studied by Durbach and Parker (2009), Durbach, Katshunga and Parker (2013), Senekal and Stemmet (2014) and Williams et al. (2016).
Williams et al. (2016, p. 137) end their paper with a suggestion that ‘the role which banks play in providing connectivity in networks could be investigated’. The current study follows these noted studies by analysing the connections of the major South African banks, namely Barclays Africa Group Ltd (changed to ABSA Group Limited in July 2018), Nedbank Group Ltd, Standard Bank Group Ltd and FirstRand Ltd, in the company director network on the JSE, but with some key differences. Unlike Durbach and Parker (2009), who conduct a macro-level analysis by investigating the topological properties of the company director network, and Durbach et al. (2013), who investigated community formation in this network using the concept of modularity and therefore take a meso-level approach, we conduct a node-level analysis that analyses key role players in the JSE company director network. Our study is therefore more comparable to Senekal and Stemmet’s (2014) node-level analysis of the company director network around the South African banking industry, but we do not limit our analysis to one sector and rather study the entire company director network on the JSE. In addition, the current study focuses on the ties between companies rather than individuals; unlike Senekal and Stemmet (2014), we follow Durbach and Parker (2009) and Durbach et al. (2013), as well as overseas studies, in analysing the company director network as a single-mode network rather than the bipartite network studied in Senekal and Stemmet (2014). Furthermore, unlike, for instance, Durbach and Parker (2009), we study this network not only as a binary network but also as a weighted network. For this analysis, we use the classic centrality measures as formalised by Freeman (1977), namely degree-, betweenness- and closeness centrality, as well as Barrat, Barthélémy and Vespignani (2004) strength. Our objective is to investigate whether the four major banks constitute key companies in this network in South Africa, as well as to which companies they have direct links.
Data
In following Durbach and Parker (2009) and Durbach et al. (2013), the McGregor BFA database was used for the current study. However, Durbach and Parker (2009) and Durbach et al. (2013) used data from March 2008, whereas the current study uses data from April 2015. We use data from 2015, because the current study was conducted in 2017, and data from 2016 were not yet available.
A complex network approach to company director networks
Although network theory (also referred to as ‘graph theory’) was already mentioned by Von Bertalanffy (1968, p. 21, 90; 1972, p. 416) as a subcategory of general systems theory, this theoretical approach has only become an important paradigm in the study of complex systems and interconnected phenomena since the late nineties. The two seminal publications that sparked the avalanche of research into complex networks were those of Watts and Strogatz (1998) and Barabási and Albert (1999), who developed the small world network model and the scale-free network model, respectively. Subsequent publications investigated similar topological features of various complex networks, including company director networks, of which Davis et al. (2003) is one of the most cited examples globally and Durbach and Parker (2009) is an example from a South African context.
A network (also referred to as a graph) consists of nodes or vertices (n) and their ties (also referred to as edges or links) (m). A company director network is usually studied as a bipartite network, where two types of vertices can be distinguished: companies and directors. Often referred to as an affiliation network, company director networks are studied in a similar way to co-authorship networks or film actor networks in that the bipartite network is projected to a single-mode network for analysis (Latapy, Magnien, & Del Vecchio, 2008, p. 40; Nacher & Akutsu, 2011, p. 4637). The projection can be done as in Figure 1 (adapted from Zhang et al., 2006, p. 601–602).
 |
FIGURE 1: The projection of a bipartite to a single-mode network. |
|
If Ui (i = 1, 2, …) represents a set of companies, and Li (i = 1, 2, …) a set of directors, then the thick lines connecting Ui to Li represent directors who serve on the board of a company, for example, L1, who sits on the boards of companies U1 and U2 or L2, who sits on the boards of U1 and U3. When projecting the network to a single-mode network, the ties between L1 and U1 and L2 and U1 are converted to a direct tie between L1 and L2, as indicated with the narrow line. The projection can be done in such a way that only companies or only directors remain, as shown by, for example, Davis et al. (2003), Conyon and Muldoon (2006), Durbach and Parker (2009), Heemskerk et al. (2013), Elouaer-Mrizak and Chastand (2013) and Drago et al. (2015). The edge between directors will then mean, ‘serve together on a board’, while an edge between companies will mean ‘share directors’. Although the projection from a bipartite to single-mode network necessarily entails a loss of information, this procedure is standard when analysing bipartite networks (Borgatti & Everett, 1997, p. 248; Durbach & Parker, 2009, p. 16; Latapy et al., 2008, p. 34; Newman, 2010, p. 125).
Edges between vertices can be indicated in a binary manner, specifically, the presence or absence of an edge is simply indicated regardless of the strength or direction of the edge. However, more information can be encoded in the network if edges are weighted, as Barrat et al. (2004, p. 3747) argue: ‘the heterogeneity in the intensity of connections may be very important in the understanding of social systems’. The same applies to a company director network; it is significant, for instance, that African Rainbow Min Ltd and Sanlam Ltd not only share directors (as would be indicated in a binary network), but also that they share five directors (as indicated with weighted edges), because five shared directors of course indicate a significantly stronger tie between companies than one shared director. Unlike in, for instance, Conyon and Muldoon (2006, p. 1326) and Durbach and Parker (2009, p. 16), weights were assigned to edges during the projection from bipartite to single-mode network for the current study, which facilitated the use of Barrat et al.’s (2004) refinement of Freeman’s (1977) degree centrality, namely strength (Si). The number of directors shared between companies was used to weight edges between vertices.
The direction of an edge can also be indicated, in which case the graph is known as a digraph and edges as arcs. However, for a company director network, direction is not meaningful; a director cannot sit on a board with another director without the reverse also being true, just as Company A cannot share directors with Company B without Company B sharing those same directors with Company A. For this reason, direction was not included in the analysis, as done in overseas studies such as that conducted by Takes and Heemskerk (2016). The following analysis is then for an undirected, but weighted, graph or network.
When constructed as a network, the JSE company director network as studied here consists of 4346 nodes (companies and directors) and 5397 edges in the bipartite rendition, 307 nodes (companies) and 1832 edges in the company projection, and 4039 nodes (directors) and 53 130 ties in the director projection. As in the case with, for instance, the US corporate network as studied by Mizruchi (1982), Davis et al. (2003) and Takes and Heemskerk (2016), as well as the South African studies by Durbach and Parker (2009) and Williams et al. (2016), the vast majority of nodes are connected in this network (93.16% for the company projection and 94.33% for the director projection). This large, connected component is referred to as the giant component, and most company director network studies focus on this component. We follow their example and conduct our analysis below on the giant component.
It is customary to calculate the macro-level topological statistics for any complex network, and although our focus is not on a macro-level analysis, these statistics are shown in Table 1. This table shows the number of nodes (n), number of edges (m), average number of edges per node (<k>), clustering coefficient (C), average path length (L) and number of components for various renditions of the JSE company director network as studied here. Average path length refers to the average shortest path (also called the geodesic path or distance) that connects any two nodes in the network, where the latter refers to ‘the smallest number of edges in the graph that must be traversed to reach one node from the other’ (Durbach & Parker, 2009, p. 17; see also Williams et al., 2016, p. 123). Average path length is calculated with Equation 1 (Kӧnig & Battiston, 2009, p. 32):
where dij is the geodesic distance from node i to node j.
| TABLE 1: Macro-level statistics for the Johannesburg Stock Exchange company director network. |
Clustering refers to the number of neighbours of a node (those with direct connections to a node) that also have a connection (Durbach & Parker, 2009, p. 17; Williams et al., 2016, p. 123). Two main formulations exist (Durbach & Parker, 2009, p. 17; Newman, 2010, pp. 198–201), but we prefer the formulation also known as transitivity that compares the ratio between the number of triangles (∆) (where an edge exists between the neighbours of node i) and triples (˅) (where no edge exists between the neighbours of node i) (see also Durbach & Parker, 2009, p. 17), as given by Equation 2 (Latapy et al., 2008, p. 458):
Table 1 shows that every rendition of the JSE company director network is also characterised by a short average path length, as found in previous studies (e.g. Durbach & Parker, 2009). The average clustering or transitivity is also high for the director projection of this network, again in line with previous findings on company director networks (e.g. Durbach & Parker, 2009). However, our focus is on centrality in this network, as discussed in the rest of the article.
Centrality measures
One of the earliest applications of network theory was to identify key players in networks (Estrada, 2012, p. 121). A variety of centrality measures have been developed within network theory over the last century, including eigenvector centrality (Bonacich, 1987), hyperlink-induced topic search (Kleinberg, 1999), PageRank (Brin & Page, 1998) and others. The classic centrality measures used in network theory are, however, those formalised by Freeman (1977), namely degree (CD), betweenness (CB) and closeness centrality (CC) (although Freeman, 1977, p. 35 admits that he based his betweenness centrality on the ‘intuition’ of the anthropologist Bavelas, 1948). These three centrality measures, however, do not take the weight of edges into account, and hence strength (Si) was developed by Barrat et al. (2004) as a refinement of degree centrality. The current study uses CD, CB, CC and Si.
Degree centrality
Degree centrality (CD) is the simplest centrality measure and calculates the number of direct ties a node has with its neighbours. This form of centrality is the oldest application of centrality measures to company director networks (Takes & Heemskerk, 2016, p. 4). A node with a high degree centrality is usually a very active node in a network (Senekal & Stemmet, 2014, p. 967), and in some cases CD can identify important nodes as well. In De Benedictis and Tajoli’s (2011) study of the World Trade Network (WTN), for instance, the UK had the highest degree of centrality in 1980 and the USA in 2000, and both are of course important as well as active role players in this network. Similarly, in a citation network, CD will highlight the most cited papers and authors, and the number of citations is generally considered a measure of importance in a citation network. In general, however, CD is more an indication of activity than of importance. In the case of the company director network, CD for the bipartite version of the network will indicate which companies have the highest number of directors and which directors sit on the highest number of boards. For the single-mode projection of the network, degree centrality will indicate which directors sit on boards with the highest number of other directors, while for the company projection degree, centrality will identify the companies that share directors with the largest number of other companies.
Degree centrality (CD) is calculated with Equation 3 for node i (Piccardi et al., 2010, p. 5248; Prell, 2012, p. 97; Elouaer-Mrizak & Chastand, 2013, p. 87):
In Equation 3, xij indicates the value of the tie between nodes i and j (0 or 1), and N indicates the number of nodes in the network.
Table 2 indicates the 20 companies in the single-mode projection of the company director network on the JSE that have the highest degree centrality. Anglo American Platinum Ltd has ties with 56 other companies through its board of directors, which makes it the highest connected company, while Telkom SA Soc Ltd has the second-highest number of ties with other companies (49) and MMI Holdings has the third-highest number of ties (48). Because ‘these networks of board interlocks … facilitate the spread of governance routines and practices, the exchange of resources, communication and the dissemination of new ideas’ (Takes & Heemskerk, 2016, p. 3), such high numbers of direct ties with other companies of course put these companies in favourable positions to monitor the market and cooperate with many companies. Further, note that the four largest banks (indicated with shaded cells) are likewise high on this list (as, for instance, Farina, 2008 also found when analysing the Italian company director network), which allows the banks to obtain up-to-date information about decisions being made by numerous companies listed on the JSE and to advise several companies. Their high position on the list of companies with the highest degree of centrality is then the first indication that the four major banks play an important role in the South African company director network.
Closeness centrality
Closeness centrality (CC) identifies those nodes that can on average reach any other node with a short path (Senekal & Stemmet, 2014, p. 968; Takes & Heemskerk, 2016, p. 5; De Benedictis et al., 2013, p. 28). Of course, nodes that can on average reach any other node with a short path can be found in the core of a network; hence, closeness centrality is furthermore an indication of which nodes function in the centre of a network. In this sense, closeness centrality has the closest meaning to the colloquial meaning of centrality, namely ‘at the centre’, whereas the other centrality measures are rather an indication of activity (degree centrality) or bridging roles (betweenness centrality). Nodes at the centre of a network are also usually more established and influential nodes (Csermely, London, Wu, & Uzzi, 2013, p. 111), which also applies to corporate board networks; centrally located actors tend to have high levels of status and power (Mizruchi, 2007, p. 12). Closeness centrality (CC) is calculated with Equation 4 for node i (Prell, 2012, p. 108):
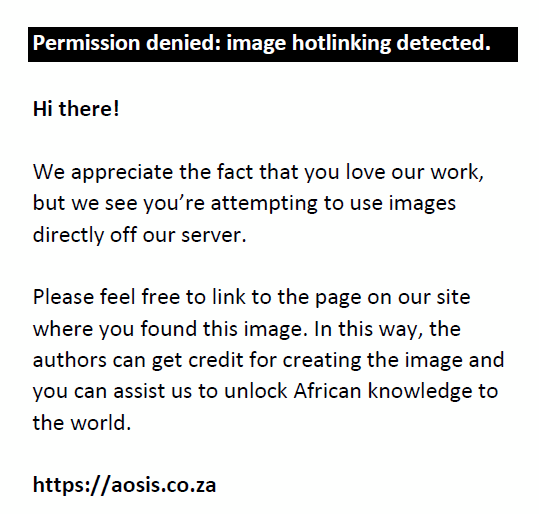
In Equation 4, dij indicates the distance (in terms of network topology, not Euclidean space) that separates nodes i and j, while N again indicates the number of nodes in the network.
Table 2 provides the closeness centrality rankings of the top 20 companies on the JSE. Note that because absolute values mean little to the reader in this case (closeness centrality figures are indicated in the spectrum 0 ≤ CC ≤ 1 but are relative to the network’s topology; Takes & Heemskerk, 2016, p. 6), rankings are preferred here when discussing closeness and betweenness centralities (which also lies within the same spectrum). Further, note that a competitive ranking is used here, where two identical numbers are given the same ranking and the next value receives a ranking as in the sequence [1, 2, 2, 4]. Because nodes with a high closeness centrality score function in the core of a network, Table 3 shows that MMI Holdings Ltd and Telkom SA Soc Ltd are at the core of the JSE company director network. These companies’ central position creates the potential for information to reach them in the shortest path and for them to spread information throughout the network in the shortest path. Note again that the four largest banks are in the top 10, which illustrates that they function at the core of this network, with similar advantages to the other companies with the highest closeness centrality scores. This finding is also in line with numerous previous studies that found banks to function within the core of the corporate network (e.g. Bearden et al., 1975; Mintz & Schwartz, 1985; Mizruchi, 1982).
| TABLE 3: Companies with ties with three and four of the major four banks. |
Betweenness centrality
Betweenness centrality measures to what extent short paths flow through a node (Farina, 2008, p. 9; Senekal & Stemmet, 2014, p. 967; Takes & Heemskerk, 2016, p. 5). Because nodes on a short path can often influence the flow of information or resources and occupy a bridging position, betweenness centrality is generally considered to be the centrality measure that identifies the most important nodes in a network (Caldarelli, 2013, p. 253; Prell, 2012, p. 107; De Benedictis et al., 2013, p. 24). In De Benedictis and Tajoli’s (2011, p. 1434) study of the WTN, the UK, for instance, had consistently had a high betweenness centrality score since the 1960s. In 1960, it had the second-highest betweenness centrality, in 1980 the highest, and in 2000 the third highest. The USA was third in 1960, seventh in 1980 and first in 2000 (along with Germany). Farina (2008) also found that banks generally score high on betweenness centrality when analysing the company director network in Italy. Betweenness centrality is calculated with Equation 5 for node k (Prell, 2012, p. 105):
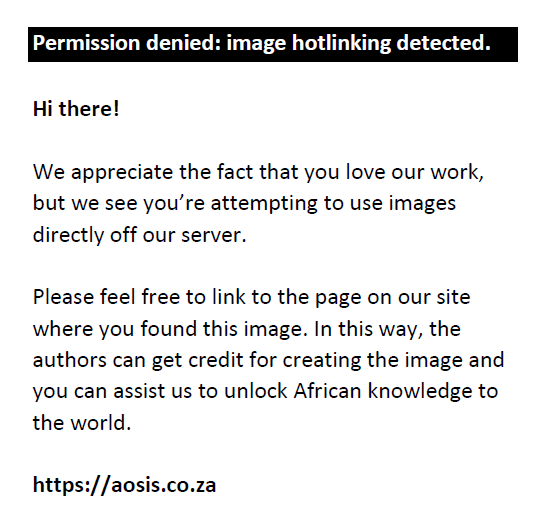
In Equation 5, ∂ikj indicates the number of short paths connecting nodes i and j that run through node k, while ∂ij indicates the number of short paths connecting nodes i and j.
Table 2 shows the 20 companies on the JSE with the highest betweenness centrality scores, again as expressed as a ranking rather than an absolute number. Note again that the Standard Bank Group Ltd and Nedbank Group Ltd are in the top 10, while Barclays Africa Group Ltd (ABSA Group Limited) has the 13th-highest betweenness centrality score. Three of the four major banks are therefore in the top 20, with the notable exception of FirstRand Ltd, which has the 37th-highest betweenness centrality score. Most of the four major banks therefore provide key meeting places and function in bridging roles in the JSE company director network. Betweenness centrality, in this instance, means that if information were to flow along social ties, the companies with the highest betweenness centrality scores would provide key meeting places to facilitate the flow of information in the network.
Strength
However, degree-, betweenness- and closeness centralities do not take the weight of edges into account. Because the weight of edges can also influence the importance of nodes in a network, Barrat et al. (2004, p. 3748) developed a weighted counterpart of degree centrality, namely strength (Si). In their calculations, strength, for instance, identified the most important airports in the World Airline Network. Strength is calculated for node i using Equation 6 (Barrat et al., 2004).
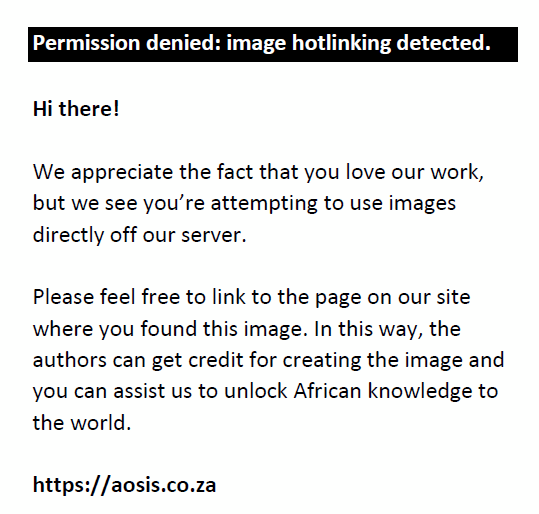
In Equation 6, xij indicates the value of the tie between node i and j (0 or 1) (as in Equation 3), and wij indicates the weight of the tie between nodes i and j. In the network studied here, wij therefore indicates the number of directors shared by two companies (for the company projection of the network). In essence, strength calculates the number of ties a company has but also takes into account how many directors are shared between two companies.
Table 2 provides a list of the 20 companies that rank highest on strength, again represented as a ranking. Note that FirstRand Ltd has the highest strength of all four major banks but that all four major banks are in the top 10. In plain terms, these companies are important, because they share many directors with other companies, although – unlike in the case of degree centrality – strength also considers the fact that some ties between companies are stronger than others.
Degree-, betweenness- and closeness centrality, and closeness centrality, as well as strength, all measure importance in a network from a different perspective, and in all four cases, the major four banks can be shown to occupy important roles in the South African company director network. When combined, all four measures together provide a clearer picture of which companies fulfil important roles in this network, just as Krebs (2002, p. 47) and Roberts and Everton (2011, p. 11) use degree-, betweenness- and closeness centrality together to identify the leading figures in terrorist networks. Table 2 provides a summary of companies’ rankings on degree-, betweenness- and closeness centrality, as well as strength. For each company, their rankings on each centrality measure were converted to an overall ranking. For instance, Standard Bank Group Ltd ranked seventh on betweenness, fourth on closeness, fourth on degree and sixth on strength, but overall, when all four centrality measures are combined this company ranks fourth of all companies. The four major banks are highlighted in Table 2.
When combined, FirstRand Ltd ranks lower in general on these four centrality measures than Barclays Africa Group Ltd (ABSA Group Limited), Nedbank Group Ltd and Standard Bank Group Ltd do, although it ranks higher in strength. Overall, Barclays Africa Group Ltd (ABSA Group Limited) and Nedbank Group Ltd have the same ranking, while Standard Bank Group Ltd ranks highest overall of the banks. Note, however, that all four banks rank within the top 20 companies overall and, apart from FirstRand Ltd, also in the top 10. This high overall ranking indicates the important role played by these four banks in connecting South African companies by providing contact between different companies and facilitating the spread of information.
The central role played by the big four banks in the South African company director network can be illustrated visually by using the Fruchterman and Reingold (1991) force-directed layout algorithm. Like other force-directed layout algorithms, Fruchterman and Reingold (1991) position the most important nodes in the centre of the network, while less important nodes are positioned on the periphery because of their lack of important edges (Kobourov, 2013, p. 397). As Figure 2 shows, whether the bipartite (left) or single-mode version (right) is used, the four major banks are positioned at the core of the company director network. Banks are indicated with darker nodes.
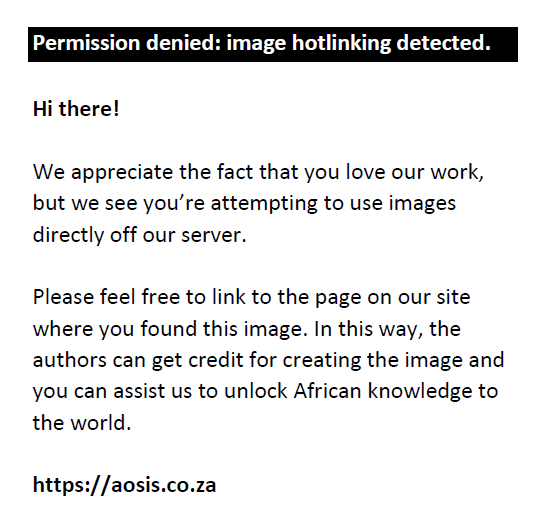 |
FIGURE 2: The four major South African banks in the company director network on the Johannesburg Stock Exchange, using the bipartite (a) and single-mode projections (b). |
|
Based on their high positions when using the four centrality measures discussed in this article, as well as a combination of these centrality measures and their position in the core of the JSE company director network when using the Fruchterman and Reingold (1991) force-directed layout algorithm, the four major banks in South Africa can be shown to occupy key positions in the JSE company director network. The rest of the article considers their direct connections to provide more detail about which companies they are directly linked to.
Banks’ direct ties in the Johannesburg Stock Exchange director network
The four major banks each have different direct ties with other companies via the company director network but overlap to a significant extent. FirstRand has ties with 38 companies: Adcorp Holdings Limited; AECI Limited; African Rainbow Min Ltd; Allied Electronics Corp; Anglo American Plat Ltd; Ardor Sa Ltd; Aveng Group Limited; Avi Ltd; British American Tob Plc; Caxton CTP Publish Print; Discovery Ltd; Distell Group Ltd; Emira Property Fund; Eqstra Holdings Ltd; Grindrod Ltd; Illovo Sugar Ltd; JSE Ltd; Lewis Group Ltd; Massmart Holdings Ltd; Mediclinic Internat Ltd; Metrofile Holdings Ltd; MMI Holdings Limited; Mr Price Group Ltd; Nampak Ltd; Naspers Ltd; Oceana Group Ltd; Pick n Pay Stores Ltd; Rand Merchant Ins Hldgs; RCL Foods Limited; Remgro Ltd; RMB Holdings Ltd; Santam Limited; Sun International Ltd; Telkom SA Soc Ltd; Tiger Brands Ltd; Tongaat Hulett Ltd; Trans Hex Group Ltd and Vukile Property Fund Ltd.
Nedbank has ties with 43 companies: Adcock Ingram Hldgs Ltd; AECI Limited; African Rainbow Min Ltd; Afrox Oxygen Limited; Anglo American Plat Ltd; Anglo American Plc; ArcelorMittal SA Ltd; Aveng Group Limited; Barloworld Ltd; Brait SE; Datatec Ltd; Delta Property Fund Ltd; Exxaro Resources Ltd; Goliath Gold Mining Ltd; Harmony GM Co Ltd; Hulamin Ltd; JSE Ltd; Kap Industrial Hldgs Ltd; Liberty Holdings Ltd; Life Healthcare Grp Hldgs Ltd; Lonmin Plc; MMI Holdings Limited; Nampak Ltd; Oceana Group Ltd; Old Mutual Plc; PPC Ltd; RCL Foods Limited; Remgro Ltd; Sabmiller Plc; Sanlam Limited; Santam Limited; Sasol Limited; Sephaku Holdings Ltd; Sibanye Gold Limited; South Ocean Holdings Ltd; Stefanuti Stck Hldgs Ltd; Telkom SA Soc Ltd; Tiger Brands Ltd; Tongaat Hulett Ltd; Tsogo Sun Holdings Ltd; Vodacom Group Ltd; Winhold Ltd and Woolworths Holdings Ltd.
Barclays (ABSA) has ties with 45 companies: Advtech Ltd; African Rainbow Min Ltd; Andulela Inv Hldgs Ltd; Anglo American Plat Ltd; Aspen Pharmacare Hldgs Ltd; Aveng Group Limited; Barloworld Ltd; BHP Billiton Plc; Clicks Group Ltd; Clover Industries Ltd; Datatec Ltd; Distell Group Ltd; Efficient Group Ltd; Eqstra Holdings Ltd; Evraz Highveld Steel and Vanadium Ltd; Gold Fields Ltd; Harmony Gm Co Ltd; Illovo Sugar Ltd; Imperial Holdings Ltd; Italtile Ltd; Kumba Iron Ore Ltd; Liberty Holdings Ltd; Life Healthc Grp Hldgs Ltd; Metmar Ltd; Metrofile Holdings Ltd; MMI Holdings Limited; Mtn Group Ltd; Naspers Ltd; Northam Platinum Ltd; Oceana Group Ltd; Pioneer Foods Group Ltd; RCL Foods Limited; Remgro Ltd; Reunert Ltd; Sanlam Limited; Santam Limited; Sappi Ltd; Sasol Limited; Steinhoff Int Hldgs Ltd; Sun International Ltd; Tiger Brands Ltd; Tongaat Hulett Ltd; Trans Hex Group Ltd; Vodacom Group Ltd and Vukile Property Fund Ltd.
Standard Bank has ties with 46 companies: AECI Limited; African Rainbow Min Ltd; Afrox Oxygen Limited; Allied Electronics Corp; Anglo American Plat Ltd; Anglo American Plc; Anglogold Ashanti Ltd; ArcelorMittal SA Limited; Ascension Prop Ltd A; Assore Ltd; Aveng Group Limited; Brimstone Inv Corp Ltd; City Lodge Hotels Ltd; Gold Fields Ltd; Harmony GM Co Ltd; Illovo Sugar Ltd; Imperial Holdings Ltd; JD Group Ltd; Liberty Holdings Ltd; Mediclinic Internat Ltd; Metair Investments Ltd; Metmar Ltd; Mondi Ltd; Mondi Plc; Mr Price Group Ltd; MTN Group Ltd; Nampak Ltd; Naspers Ltd; Netcare Limited; Petmin Ltd; PPC Limited; Randgold and Expl Co Ltd; Remgro Ltd; Reunert Ltd; Rockwell Diamonds Inc; Royal Bafokeng Platinum; Sabmiller Plc; Sasol Limited; Sentula Mining Ltd; Sibanye Gold Limited; Sun International Ltd; Tiger Brands Ltd; Tongaat Hulett Ltd; Village Main Reef GM Co; Wesizwe Platinum Ltd and Woolworths Holdings Ltd.
Figure 3 shows how intricately connected this network is.
 |
FIGURE 3: The network of companies with direct links to the four banks. |
|
Overall, 104 companies out of 307 are directly linked to the four major banks. However, it is not simply the number of connections that result in the four major banks’ central roles in this network but also the companies they have ties with; these are usually the companies at the core of this network as well (such as Anglo American Platinum). Table 3 shows the overall centrality of companies with ties with banks. Companies with ties with all four of the major banks are indicated with a dark shade, while the rest of the companies on this table have ties with three of the major banks.
Conclusion
Company networks are one of the ways in which information spreads in an economy. This article has shown how central the four major banks are to the South African company director network. Whether the classic centrality measures (i.e. degree-, betweenness- and closeness centrality) or the weighted equivalent of degree (strength) is used, the major banks are always ranked among the most important companies on the JSE. In addition, all four centrality measures were combined, and it was shown that the four major banks then also occupy key positions in this network. Even if simply a force-directed layout algorithm like that of Fruchterman and Reingold (1991) is used, these four companies can again be shown to function at the core of the company director network. Overall, a network analysis offers various tools to investigate whether banks occupy a central position in the company director network in South Africa as they do in other companies, and regardless of which measure is used, the current study finds that they do occupy key positions in this network. This position of centrality puts the big four banks in a favourable position to share information and influence decisions that impact on the heart of the South African economy.
While the study of director networks illustrates valuable aspects of the functioning of an economy, one type of economic network that has not been studied in a South African context, but has been done overseas, is the shareholder network. Shareholder networks are networks where ownership instead of information flows; hence, a considerable amount of effort has been invested into investigations that analysed shareholder networks (e.g. Glattfelder, 2013). A future study should explore how the JSE network is connected in terms of shareholder relations.
Acknowledgements
Competing interests
The authors declare that they have no financial or personal relationships that may have inappropriately influenced them in writing this article.
Authors’ contribution
B.A.S. was responsible for the research design, literature review, data analysis and writing. K.S. made conceptual contributions and aided in data analysis and writing.
References
Abdollahian, M., Thomas, J., Yang, Z., & Chiang, R. (2017). Making relationships matter: Director interlocks and fortune 500 performance, 1996–2007. In J. Kantola, T. Barath, S. Nazir & T. Andre (Eds.), Advances in human factors, business management, training and education. Advances in intelligent systems and computing (vol. 498, pp. 1159–1169). Cham: Springer.
Barabási, A.-L., & Albert, R. (1999). Emergence of scaling in random networks. Science, 286, 509–511. https://doi.org/10.1126/science.286.5439.509
Barrat, A., Barthélémy, M., & Vespignani, A. (2004). The architecture of complex weighted networks. Proceedings of the National Academy of Sciences, 101, 3747–3752. https://doi.org/10.1073/pnas.0400087101
Bavelas, A. (1948). A mathematical model for group structure. Applied Anthropology, 7, 16–30. https://doi.org/10.17730/humo.7.3.f4033344851gl053
Bearden, J., Atwood, W., Freitag, P., Hendricks, C., Mintz, B., & Schwartz, M. (1975). The nature and extent of bank centrality in corporate networks. Paper presented at the Annual Meeting of the American Sociological Association. In J. Scott (Ed.), Social Network; Critical Concepts in Sociology, Volume III (n.p.). London: Taylor & Francis.
Bonacich, P. (1987). Power and centrality: A family of measures. The American Journal of Sociology, 92, 1170–1182. https://doi.org/10.1086/228631
Borgatti, S. P., & Everett, M. G. (1997). Network analysis of 2-mode data. Social Networks, 19, 243–269. https://doi.org/10.1016/S0378-8733(96)00301-2
Brin, S., & Page, L. (1998). The anatomy of a large-scale hypertextual web search engine. In: Proceedings of the seventh International Conference on the World Wide Web, 14–18 April 1998, (pp. 107–117), Brisbane, Australia: n.p. https://doi.org/10.1016/S0169-7552(98)00110-X
Caldarelli, G. (2013). Scale free networks. Complex webs in nature and technology. Oxford: Oxford University Press.
Conyon, M. J., & Muldoon, M. R. (2006). The small world of corporate boards. Journal of Business Finance and Accounting, 33(9/10), 1321–1343. https://doi.org/10.1111/j.1468-5957.2006.00634.x
Csermely, P., London, A., Wu, L.-Y., & Uzzi, B. (2013). Structure and dynamics of core/periphery networks. Journal of Complex Networks, 1, 93–123. https://doi.org/10.1093/comnet/cnt016
Davis, G., & Greve, H. (1997). Corporate elite networks and governance changes in the 1980s. American Journal of Sociology, 103, 1–37. https://doi.org/10.1086/231170
Davis, G. F., Yoo, M., & Baker, W. E. (2003). The small world of the American corporate elite, 1982–2001. Strategic organization, 1(3), 301–326. https://doi.org/10.1177/14761270030013002
De Benedictis, L., & Tajoli, L. (2011). The world trade network. The World Economy, 34(8), 1417–1454. https://doi.org/10.1111/j.1467-9701.2011.01360.x
De Benedictis, L., Nenci, S., Santoni, G., Tajoli, L., & Vicarelli, C. (2013). Network analysis of world trade using the BACI-CEPII dataset. CEPII Working Paper, 1–60. Paris: CEPII.
Drago, C., Millo, F., Ricciuti, R., & Santella, P. (2015). Corporate governance reforms, interlocking directorship and company performance in Italy. International Review of Law and Economics, 41, 38–49. https://doi.org/10.1016/j.irle.2014.09.003
Drago, C., & Ricciuti, R. (2017). Communities’ detection as a tool to assess a reform of the Italian interlocking directorship network. Physica A: Statistical Mechanics and its Applications, 466, 91–104. https://doi.org/10.1016/j.physa.2016.08.029
Durbach, I., & Parker, H. (2009). An analysis of corporate board networks in South Africa. South African Journal of Business Management, 40(2), 15–26.
Durbach, I., Katshunga, D., & Parker, H. (2013). Community structure and centrality effects in the South African company network. South African Journal of Business Management, 44(2), 35–43. https://doi.org/10.4102/sajbm.v44i2.154
Elouaer-Mrizak, S., & Chastand, M. (2013). Detecting Communities within French Intercorporate Network. Procedia - Social and Behavioral Sciences, 79, 82–100. https://doi.org/10.1016/j.sbspro.2013.05.058
Estrada, E. (2012). The structure of complex networks. Theory and applications. Oxford: Oxford University Press.
Farina, V. (2008). Banks’ centrality in corporate interlock networks: Evidences in Italy. MPRA Paper, 11698. Munich: Munich University Library.
Freeman, L. C. (1977). A set of measures of centrality based on betweenness. Sociometry, 40, 35–41. https://doi.org/10.2307/3033543
Friel, N., Rastelli, R., Wyse, J., & Raftery, A. E. (2016). Interlocking directorates in Irish companies using a latent space model for bipartite networks. PNAS, 113(24), 6629–6634. https://doi.org/10.1073/pnas.1606295113
Fruchterman, T. M., & Reingold, E. M. (1991). Graph drawing by force-directed placement. Software: Practice and experience, 21(11), 1129–1164. https://doi.org/10.1002/spe.4380211102
Glattfelder, J. B. (2013). Decoding Complexity: Uncovering Patterns in Economic Networks. Heidelberg: Springer.
Guo, C., & Lv, P. (2018). Network position of independent director in cross-border mergers and acquisitions, International Journal of Emerging Markets, 13(1), 118–135. https://doi.org/10.1108/IJoEM-01-2017-0027
Heemskerk, E., & Schnyder, G. (2008). Small states, international pressures, and interlocking directorates: The cases of Switzerland and the Netherlands. European Management Review, 5(1), 41–54. https://doi.org/10.1057/emr.2008.3
Heemskerk, E. M. (2013). The rise of the European corporate elite: Evidence from the network of interlocking directorates in 2005 and 2010. Economy and Society, 42(1), 74–101. https://doi.org/10.1080/03085147.2012.686720
Heemskerk, E. M., Daolio, F., & Tomassini, M. (2013). The Community Structure of the European Network of Interlocking Directorates 2005–2010. PLoS One, 8(7), e68581. https://doi.org/10.1371/journal.pone.0068581
Jeidels, O. (1905). Das Verhältnis der Deutschen Grossbanken zur Industrie mit besonderer Berücksichtigung der Eisenindustrie. s.l.: Duncker and Humblot.
Kleinberg, J. (1999). Authoritative sources in a hyperlinked environment. Journal of the ACM, 46, 604–632. https://doi.org/10.1145/324133.324140
Kobourov, S. G. (2013). Force-directed drawing algorithms. In: R. Tamassia (ed.), Handbook of graph drawing and visualization (pp. 383–408). s.l.: CRC Press.
Kogut, B., & Belinky, M. (2008). Comparing small world statistics over time and across countries: An introduction to the special issue comparative and transnational corporate networks. European Management Review, 5(1), 1–10. https://doi.org/10.1057/emr.2008.6
Krebs, V. E. (2002). Mapping networks of terrorist cells. CONNECTIONS, 24(3), 43–52.
Kӧnig, M. D., & Battiston, S. (2009). From graph theory to models of economic networks. In: A. Naimzada (ed.) Networks, topology and dynamics (pp. 23–63). Heidelberg: Springer.
Latapy, M., Magnien, C., & Del Vecchio, N. (2008). Basic notions for the analysis of large two-mode networks. Social Networks, 30, 31–48. https://doi.org/10.1016/j.socnet.2007.04.006
Mintz, B., & Schwartz, M. (1985). The power structure of American business. Chicago, IL: University of Chicago Press.
Mizruchi, M. S. (2007). Political economy and network analysis. An untapped convergence. Sociologica, 2, 1–28.
Mizruchi, M. (1982). The American Corporate Network, 1904–1974. Beverley Hills: Sage.
Nacher, J., & Akutsu, T. (2011). On the degree distribution of projected networks mapped from bipartite networks. Physica A, 390, 4636–4651. https://doi.org/10.1016/j.physa.2011.06.073
Newman, M. E. (2010). Networks. Oxford: Oxford University Press.
Piccardi, C., Calatroni, L., & Bertoni, F. (2010). Communities in Italian corporate networks. Physica A, 389, 5247–5258. https://doi.org/10.1016/j.physa.2010.06.038
Prell, C. (2012). Social Network Analysis. History, theory and methodology. London: Sage.
Raddant, M., Milaković, M., & Birg, L. (2017). Persistence in corporate networks. Journal of Economic Interaction and Coordination, 12(2), 249–276. https://doi.org/10.1007/s11403-015-0165-5
Roberts, N., & Everton, S. F. (2011). Strategies for combating dark networks. Journal of Social Structure, 12(2), 1–32.
Senekal, B. A., & Stemmet, K. (2014). The South African Banking Director Network: An Investigation Into Interlocking Directorships Using Social Network Analysis (SNA). International Business and Economics Research Journal, 13(5), 963–980. https://doi.org/10.19030/iber.v13i5.8765
Shaw, T. S., Cordeiro, J. J., & Saravanan, P. (2016). Director network resources and firm performance: Evidence from Indian corporate governance reforms. Asian Business & Management, 15(3), 165–200. https://doi.org/10.1057/s41291-016-0003-1
Sinani, E., Stafsudd. A., Thomsen, S., Edling, C., & Randøy, T. (2008). Corporate governance in Scandinavia: Comparing networks and formal institutions. European Management Review, 5(1), 27–40. https://doi.org/10.1057/emr.2008.1
Takes, F. W., & Heemskerk, E. M. (2016). Centrality in the global network of corporate control. Social Network Analysis and Mining, 6(97), 1–18. https://doi.org/10.1007/s13278-016-0402-5
Von Bertalanffy, L. (1968). General systems theory: Foundations, development, applications. New York: George Braziller.
Von Bertalanffy, L. (1972). The history and status of general systems theory. The Academy of Management Journal, 15(4), 407–426.
Watts, D. J., & Strogatz, S. H. (1998). Collective dynamics of ‘small-world’ networks. Nature, 393(6684), 409–410. https://doi.org/10.1038/30918
Williams, J. J., Deodutt, J., & Stainbank, L. J. (2016). An analysis of director interlocks on the Johannesburg Stock Exchange. South African Journal of Accounting Research, 30(2), 120–138. https://doi.org/10.1080/10291954.2015.1099203
Zhang, P.-P., Kan, C., He, Y., Zhou, T., Su, B.-B., Jin, Y., Chang, H., He, D.-R. (2006). Model and empirical study on some collaboration networks. Physica A, 360, 599–616. https://doi.org/10.1016/j.physa.2005.05.044
|